
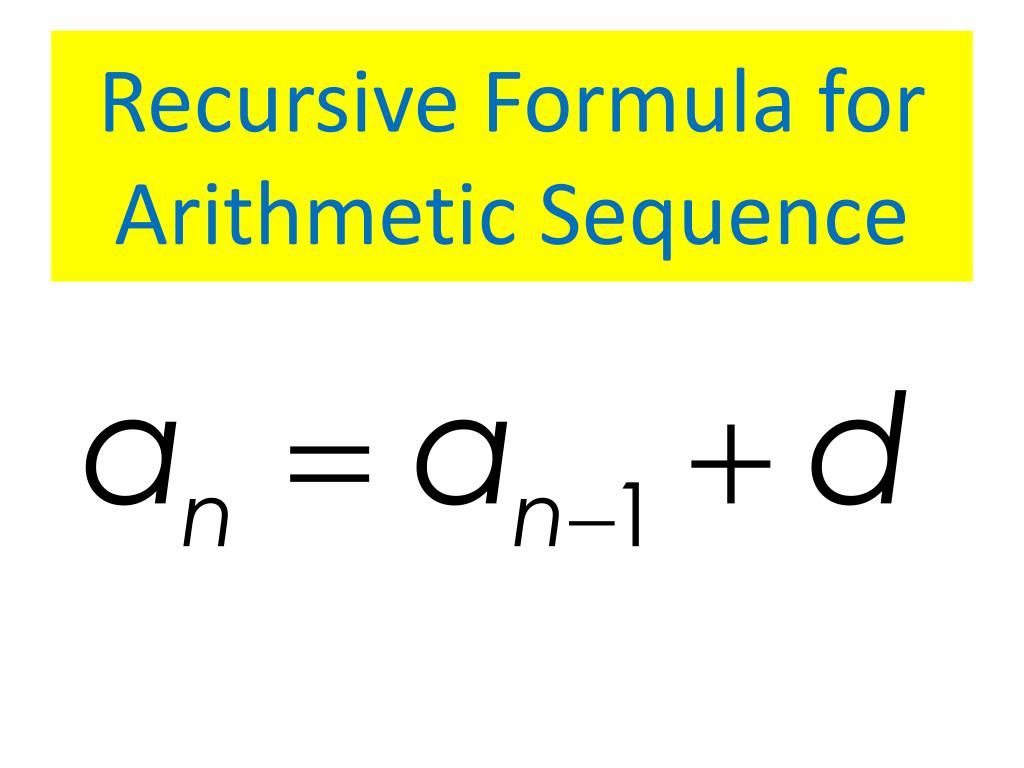
So here's your most general recursive formula, and most likely the answer you need:Ī n = -9 + 30(n-1) <- general recursive formula 9 is the first number in the sequence, and 30 is the thing being added to each termĪ 68 = -9 + (67)(30) <- do this by hand or in the calculator correctly, remembering order of operationsĪ 68 = 2001 <- better than adding 30 67 times, right? That's what the n-1 does for us. Algebra Sequence Calculator Step 1: Enter the terms of the sequence below. For example, let us set the initial term to 1, and the common ratio is set to 2. Now let us construct an equation we can use to describe geometric progression.

For instance, if we want the 68th term of the sequence (which really means we're adding 30 to the first term of the sequence 67 times), here's what we'll do:Ī 68 = (-9) + (68-1)(30) <- since we want the 68th term of the sequence. The initial number of the sequence and the common ratio are used to derive recursive and explicit formulas. The d refers to the number that keeps getting added (so here, d = 30), and n-1 is there to catapult us to some number in the sequence. This is why you might have an arithmetic sequence formula like this in your books:Ī n just refers to a number in the sequence, and a 1 is the first term of the sequence. There is a more general formula to get from the first term of the sequence to any term after it. This is the third term, or n+1 = 2 + 1, or n+1 = 3. This is the second term, or n+1 = 1 + 1, or n+1 = 2. <- This is your recursive formula to get from one term to the term right after it.
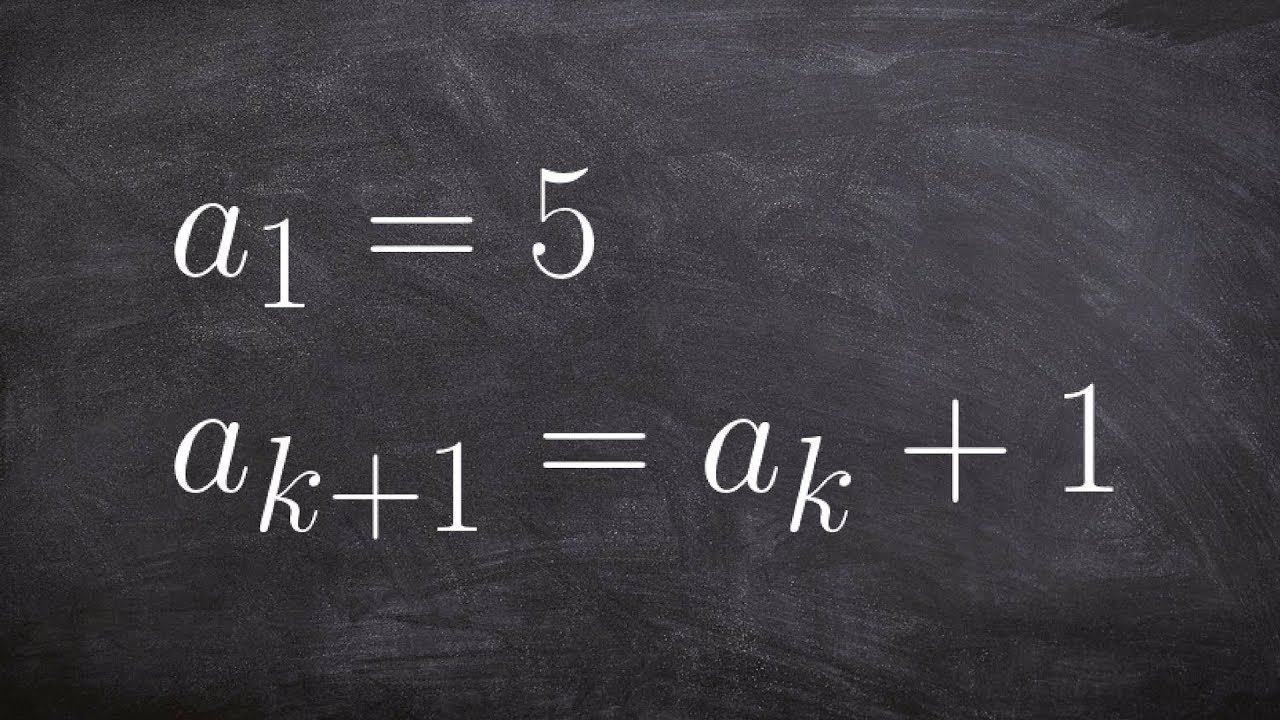
Recursive formula for sequence calculator how to#
Let a n be a term in the sequence (specifically, the n th term), and let a n+1 be the next term (one term after the previous term, hence the n + 1). This example shows how to calculate the first terms of a geometric sequence defined by recurrence. Here's how we express this mathematically: There is a pattern! 30 gets added to a term in the sequence to get the next term. We went from smaller to bigger, so perhaps the pattern here is some positive number that is added to each term. So this is an arithmetic sequence, meaning that some number (positive or negative) is added to the number before it, and that number never changes. Write a recursive formula for the sequence.


 0 kommentar(er)
0 kommentar(er)
